Plane stress and plane strain are two different approximations of the behavior of a three-dimensional object. Plane stress assumes that stresses (the forces acting on an object) act in only one plane. In contrast, plane strain assumes that both strains (the deformations caused by those stresses) and principal stresses (the maximum or minimum values of normal stress at any point) lie within one plane.
The purpose of approximations like these is to simplify calculations involving complex objects – without them, solving equations would be extremely difficult. In general, engineers will use whichever assumption will result in the simpler calculation; depending on the problem, this might be either plane stress or plane strain
Plane stress and plane strain are two-dimensional stress state that we can use to model various engineering problems. In both cases we can assume that the material behaves in a linear elastic fashion, meaning that it will return to its original shape once removing the applied stresses.
Stress vs. Strain
Before getting into planes, we need to understand the concept of stress and strain. In response to stress, a material deforms. In addition to the force applied, the material’s properties also influence the deformation amount. For example, metals are much more likely to deform under stress than ceramic materials.
Stress is the external force acting per unit area, while strain is the deformation of an object per unit length. Young’s modulus and Poisson ratio are two key concepts in elasticity, a branch of engineering that studies the relationship between applied forces and resulting deformations.
When an external force is applied to a material, it results in stresses within the material that lead to deformation or strain. The amount of stress needed to cause a strain depends on the properties of the specific material involved.
For example, brittle materials like glass will fracture at much lower stresses than ductile metals like steel.
If you want to learn a little deep into stress and it’s types, read our
Stress Formula
Stress (σ) = Force / Area
Strain Formula
Strain(ε) = change in length/original length.
Stress and Strain Relationship (Young’s Modulus equation)
E=stress/strain(ε)
where
E=Young’s modulus
Stress and Strain Curves
Stress-strain curves are very important in engineering because they tell us about a material’s behavior under loads. The stress-strain curve for a particular material is a graph of that material’s response to increasing levels of applied force or load. From the curve, we can determine how much strain (deformation) occurs at different stresses and the level of stress required to cause failure. This information is essential for designing safe and reliable structures and products.
The relationship between stress and strain is different for each material, but materials generally obey Hooke’s law when they are within their elastic range. It means that the ratio of applied stress to the resulting strain is constant over a certain range of stresses. If the material experiences stress below this yield point, it will return to its original shape once it removes the force.
If the applied stress exceeds the yield point, plastic deformation occurs, and the material will not revert to its original shape even after removing the force.
Plane Stress
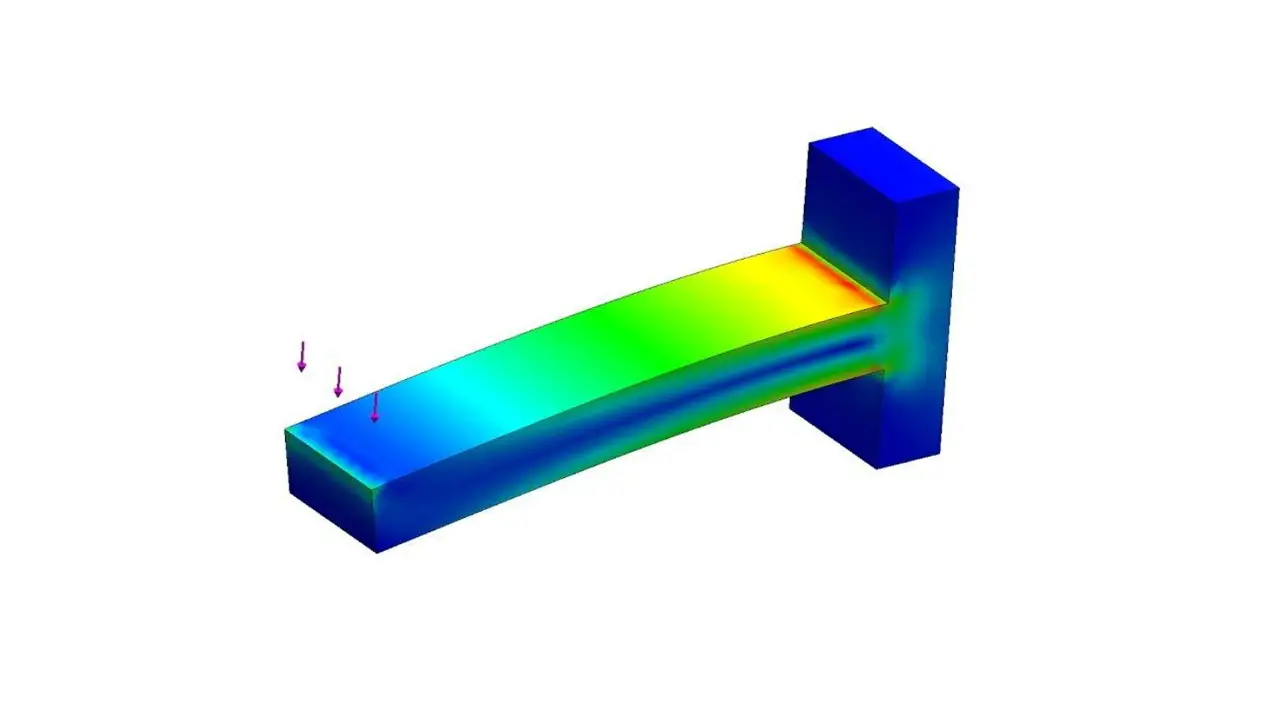
Plane stress is a state of mechanical stress where the material experiences tensile and shear stresses that act parallel to two-dimensional planes. It occurs when the third dimension experiences no or negligible stresses. Plane stress is common in thin plates and sheets, where bending forces dominate over other kinds of force.
In this context, the term “plane” refers to an imaginary plane that divides the material into thin layers. When a substance is subjected to plane stress, the stress doesn’t act evenly throughout its entire volume; instead, it’s concentrated near the surfaces perpendicular to the direction of applied force.
In-plane stress, there are two independent Stress Components, namely Normal Stress(σx), Shear Stress(τxy) & Mohr’s Circle shows relations between these components at any point within the stressed body.
Mohr’s Circle
Mohr’s circle is a graphical representation of the stress transformation equations for plane stress. The normal and shear stresses acting on various inclined planes at a point in a stressed body can be visualized using this plot.
You can also use Mohr’s circle to calculate the principal stresses, maximum shear stress, and stresses on inclined planes. The graphical representation is especially useful for visualizing the relationships between normal and shear stresses.
Plane Strain
Plane strain is a state of two-dimensional stress in which the material is free to contract or expand in one direction, but the strain is prevented from occurring in the other direction. The restrained direction is typically perpendicular to the plane of application of external forces. This stress often results from playing tug-of-war with three or more teams at once.
Plane strain is an idealized deformation state in which the strains (normal and shear) are zero in one direction. It means no stretching or compression along that axis, and all deformations occur parallel to the plane.
In this case, the term “plane” refers to an imaginary plane upon which the deformation of the material occurs. When a substance is subjected to plane strain, it experiences deformations (changes in shape or size) that are concentrated near the surfaces perpendicular to the direction of applied force.
Plane Stress vs. Plane Strain
Plane stress and plane strain measure the amount of stress on a material. It is when the stress is parallel to two planes, while a plane strain is when it’s perpendicular to one axis. The plane stress can lead to deformations, while plane strain does not.
It’s important to remember that this stress state doesn’t exist in nature. Plane strain, on the other hand, can occur in physical materials and refers to a condition where deformations are present along one axis. In contrast, the material remains undeformed along perpendicular axes.