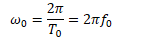Periodic signals are generated by periodic waveforms. A periodic waveform is a waveform that repeats itself at regular intervals. The most common type of periodic waveform is a sinusoidal waveform, which repeats itself every time it completes one cycle. Other types of popular periodic waveforms are square waves, triangular waves, and sawtooth waves.
When a signal repeats an exact pattern after a fixed time period, it’s considered a periodic signal. And this will continue to repeat for an infinite amount of time. The fixed time that takes to complete the repeated unit shape is known as the fundamental period T0.
Non-periodic signals do not repeat an exact pattern after a fixed time period, while periodic signals do. Non-periodic signals are spread out across a range of frequencies, while periodic signals have a constant frequency.
A continuous-time CT signal is a signal that has values for every instant of time. On the other hand, a discrete signal DT has only values for a predefined set of integers. Both the continuous-time signal and the discrete-time signals can have periodic and nonperiodic signals.
Note: A signal is an explanation of how the value of one parameter varies in relation to another parameter. In other words, a signal shows how one parameter affects another one. For example, a sinusoidal signal can be described as a function of time, where the amplitude of the signal varies with time. In this case, the time domain is the independent variable, and the amplitude is the dependent variable.
Concept
If a signal is periodic, it repeats after a fixed time period which is known as the period T. So if the function of a periodic signal is x(t), it should be the same signal after changing the time period by period T0.
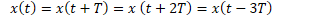
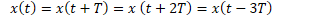

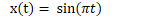
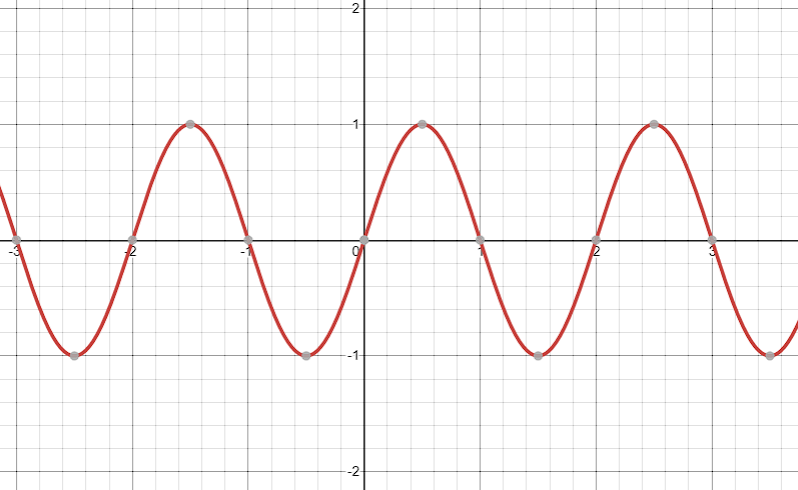
Lets consider the graphs
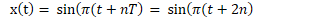
by substituting integer values for n.
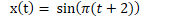
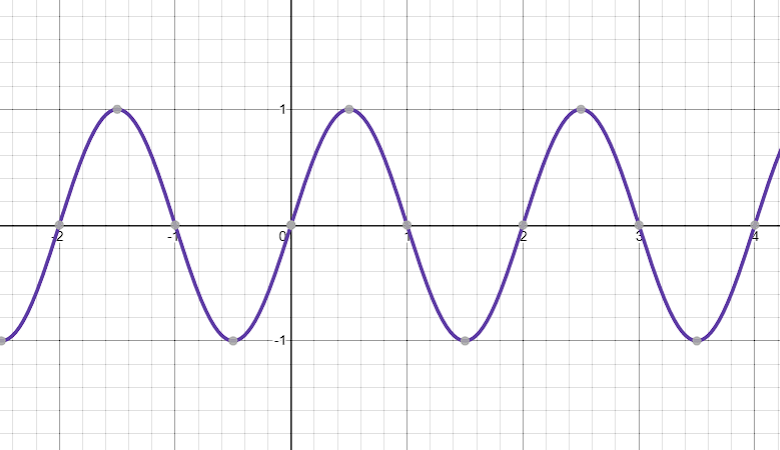
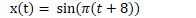
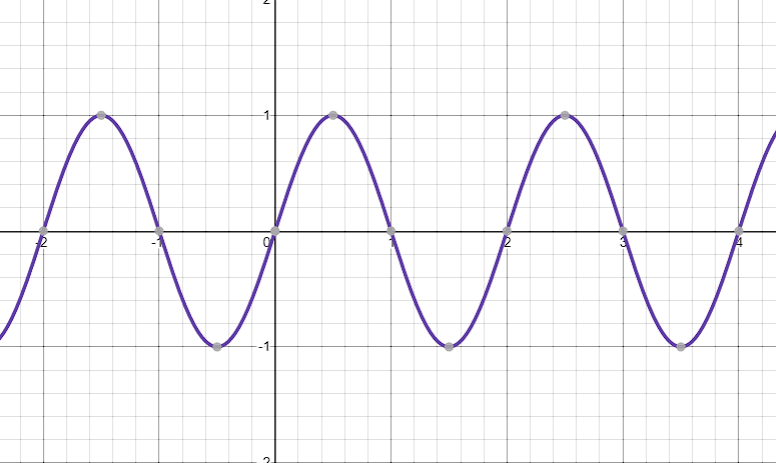
As you can see, we get the same graph for all the integer values of n.
The Periodic Signal
Every periodic signal must satisfy,
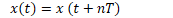
So, in order to be a periodic signal, the function of the signal must satisfy the following condition.
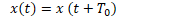
T0 is the fundamental period of the signal which is the minimum positive period of interval. The corresponding frequency and the angular frequency to the fundamental period are known as the fundamental frequency (f0) and the fundamental angular frequency (ω0).
Fundamental frequency (f0)
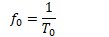
Fundamental angular frequency (ω0)