Three-phase power systems are common in industrial and commercial applications. The Star Delta Transformation theorem allows us to convert three-phase configurations between Delta and Star. In this blog post, we’ll take a look at the simplified method to apply this theorem.

Start Delta Transformation theorem states that we can convert three-phase configurations Delta to Star and Start to Delta. Here are the simplified equations of the theorem.

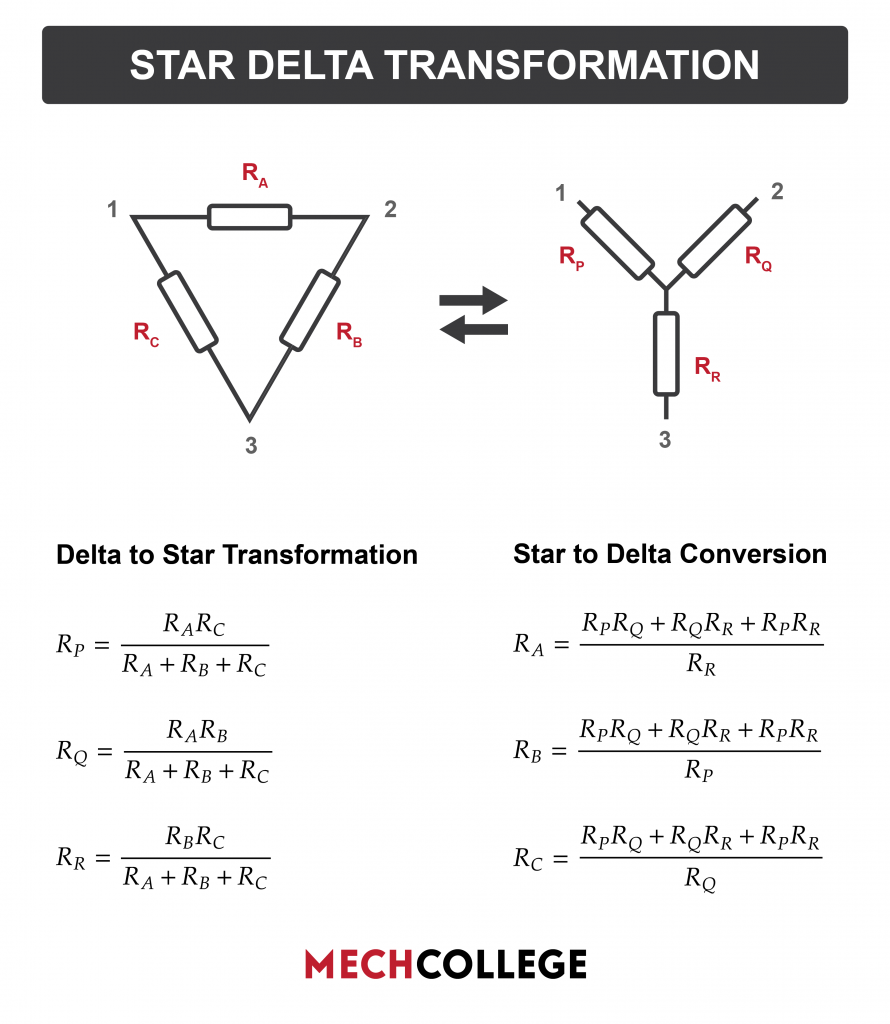
There is no need to memorize these equations to covert three-phase configurations from star to delta or delta to star. With a little understanding of the principle behind the generation of these equations, you can easily derive them.

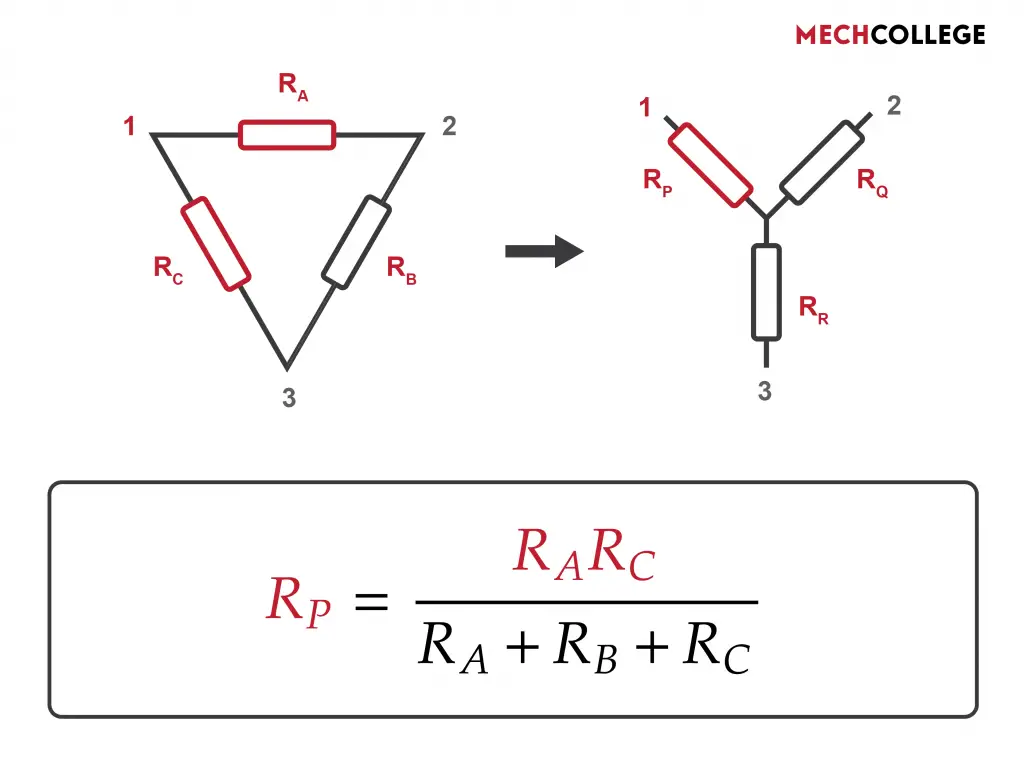
The Trick Behind Delta to Star Transformation

If the resistance of the P is the desired resistor value you need to know, look for the point related to it. In this example, it’s 1. And then go to delta configuration and find the two resistors connected to point 1, and those are resistors A and C. The multiplication of these two resistor values is the denominator. 

The numerator is the addition of all the three resistors in the delta configuration. 

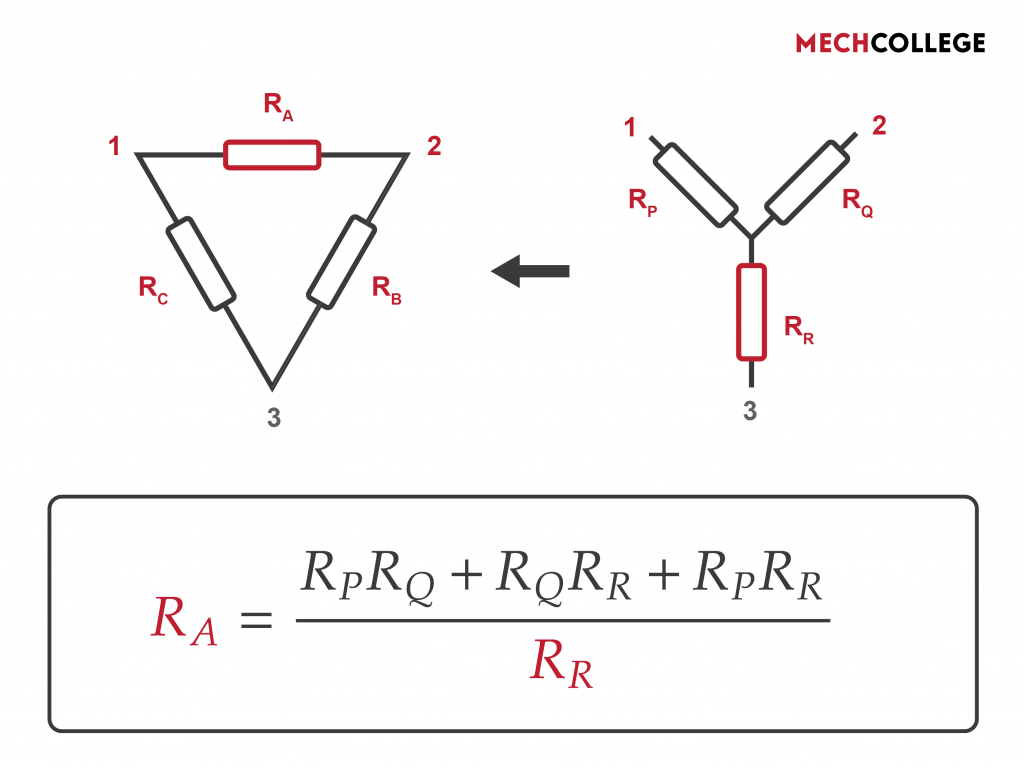
The Trick Behind Star to Delta Transformation

If you want to find the resistance of A, consider points 1 and 2. If you look at the image below, the desired resistor and the two points are colored in red. And then go to star connection and look for points 1 and 2.  Resistor P and Q are located between these points, so you need to select the opposite resistor, which is the resistance of R. The value of that opposite resistor is the denominator. 

The numerator is the same for all three equations and it also has a pattern. It’s a possible way that you can organize three resistors as pairs. Since the resistors are P, Q, and R, we can organize them as PQ, QR, and RA.  

About Post Author