The complex eigenvalues are eigenvalues that are involved with complex numbers. To understand the complex eigenvalues, you need to have a clear understanding of eigenvalues and eigenvectors.
Eigenvalue, Eigenvector and Eigenfuction
The eigenvector of a square matrix is a vector that does not change its direction under associated linear transformation. If y V is a vector, not zero, then it is an eigenvector of a square matrix. A if Av is a scalar multiple of v.
This is written as,
AV = λv
This is known as the typical eigenvalue equation.
The eigenvalue is the scaler λ which is associated with Eigenvector v. To find the eigenvalues, we need to determine the roots of the characteristic equation.
|A- λI| = 0
Eigenfunction of the operator is the set of functions that produces the same function modified and only multiplied by a constant factor.
Complex Eigenvalues (Eigenvalues of a Complex Matrix)
To find the complex eigenvalue λ, we can use the relation below.
det(A-λIn) = 0
So, first, we find the A-λIn and then we find its determinant and solve for eigenvalue λ.
Solved Example Problem
Find the eigenvalues of A ∈ Mn×n(ℂ)
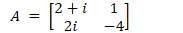
We need to come to the det(A-λI2) = 0 relationship.
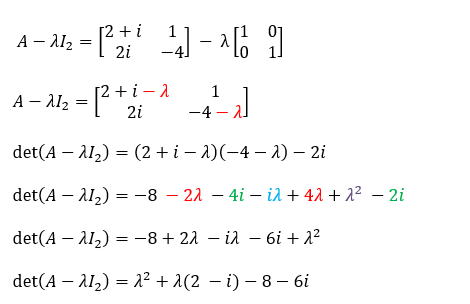
Since det(A-λI2) = 0,
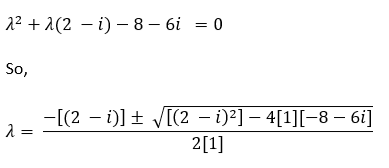
By solving the above equation, we can get the complex eigenvalue of A.


