The first thing we need to understand is why are Cauchy-Riemann (CR) Equations? What is the use of them? It’s an analysis to understand whether a complex function is complex differentiable or not in complex analysis.

Cauchy-Riemann Equations states that a complex function is differentiable if it satisfies the equations on a domain in the complex plane. There are two equations known as the Cauchy-Riemann Equations. And if both equations are true, then the complex function is complex differentiable. Furthermore, you can use the equations to find out whether a complex function is differentiable anywhere or somewhere.

The main application of Cauchy-Riemann Equations is to show a complex function is not analytic.

The Equations

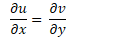
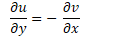
∂u/∂x =  ∂v/∂y ——–(CR Eq. 1)

∂u/∂y = – ∂v/∂x ——–(CR Eq. 2)

Proof of Cauchy–Riemann equations

Let’s take a complex number z. Since a complex number have both an imaginary part and a real part, let’s write it as,

z = x + iy

Next, let’s take a complex function of f,

f(z) = u(x,y) + iv(x,y)

And by considering f(z) is differentiable at z₀ = x₀ + iy₀

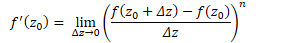
Should exsists,

With Δz = Δx + iΔy

f'(z₀) can be computed along,

C₁ : y = y₀, x>x₀, i.e.: Δz = Δx

C₂ : x = x₀, y>y₀, i.e.: Δz = iΔy

∂u/∂x =  ∂v/∂y

∂u/∂y = – ∂v/∂x

We can prove the Cauchy–Riemann equations in that way. But the proof is not required for engineering students. So, the next thing we should consider here is how can we apply this to check whether the complex function is complex differentiable.

Theorem

A necessary condition for a function f(z) = u(x,y) + iv(x,y) to be differentiable at point z₀, Cauchy–Riemann equations should be satisfied at z_0.

∂u/∂x =  ∂v/∂y

∂u/∂y = – ∂v/∂x

As a result, if the function, f(z), is analytic in an open set G, then the Cauchy–Riemann equations should be satisfied at every point of G.

Solved Example Problems

Example #1

Show that the function, f(z) = z² where z = x + iy, is differentiable at any point (anywhere).

f(z) = z²

f(z) = (x + iy)² = x² – y² + 2ixy

So,

Re(z) = u(x,y) = x² – y²

Im(z) = v(x,y) = 2xy

Note: Re(z) means real part of the function and the Im(z) means the imaginary part of the function.

By taking the partial derivatives,

∂u/∂x = 2x

∂u/∂y = -2y

∂v/∂x = 2y

∂v/∂y = 2x

In order to be the function f(z) differentiable, it should satisfy CR equations. So, let’s check that,

∂u/∂x = ∂v/∂y

∂v/∂x = – ∂u/∂y

So, the function f(z) is differentiable at any point.

Example #2

Show that the function f(z) = e^z is differentiable at any point, when z = x + iy.

f(z) = e^(x+iy)

f(z) = e^xcos(y) + ie^xsin(y)

So,

Re(z) = u(x,y) = e^xcos(y)

Im(z) = v(x,y) = e^xsin(y)

By taking the partial derivatives,

∂u/∂x = e^xcos(y)

∂u/∂y = -e^xsin(y)

∂v/∂x = e^xsin(y)

∂v/∂y = e^xcos(y)

As we can see, it satisfies CR equations.

∂u/∂x = ∂v/∂y

∂v/∂x = – ∂u/∂y

So, the function f(z) is differentiable at any point.

References

• When Is a Function That Satisfies the Cauchy-Riemann Equations Analytic? By Gray, J. D., and S. A. Morris.
• Cauchy-Riemann equations in several variables by S. J. GREENFIELD

About Post Author