When you try to find the square root of -1, something not possible with regular numbers, you’re dealing with complex numbers. These are an advanced type of number that builds on the everyday numbers we use, and they are really important for solving different kinds of math and engineering problems.
What Happens When You Square Root -1?
Normally, square roots involve positive numbers. For instance, the square root of 9 is 3, because 3 times 3 equals 9. However, things get intriguing when you consider the square root of -1. In standard mathematics, no real number multiplied by itself gives a negative product. This is where the concept of complex numbers comes into play.
Complex numbers were invented to handle situations like the square root of -1. They expand the traditional number system beyond real numbers. A complex number is made up of two parts: a real part (the kind of numbers we use daily) and an imaginary part. The imaginary part includes ‘i’, a special symbol representing the square root of -1. This means i × i = -1.
So, how do complex numbers work? They’re written as a combination of the real and imaginary parts, usually in the form a + bi. Here, ‘a’ is the real part, and ‘bi’ is the imaginary part.
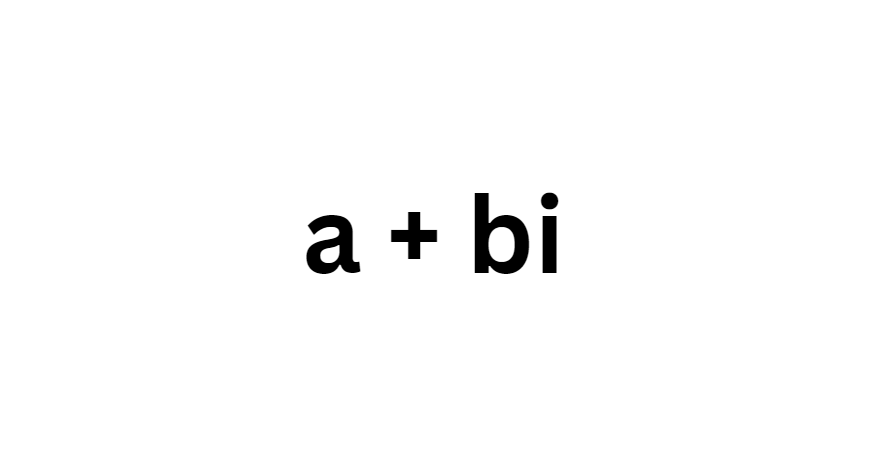
For example,
- Real Part: This is a standard number, like 2, -3, or 0.5.
- Imaginary Part: This involves taking the square root of -1, an action impossible in the realm of real numbers. This square root is denoted as ‘i’, known as the imaginary unit. So, i^2 = -1.
When we write a complex number, it looks like a + bi, where ‘a’ is the real part, and ‘bi’ is the imaginary part. For instance, 3 + 4i has a real part of 3 and an imaginary part of 4i.
Arithmetic with Complex Numbers
- Addition and Subtraction:
- Addition: Combine their real and imaginary parts separately. Adding 2 + 3i to 1 + 4i, we get (2+1) + (3i+4i), which equals 3 + 7i.
- Subtraction: Subtract the real and imaginary parts separately. So, 2 + 3i minus 1 + 4i is (2-1) + (3i-4i), resulting in 1 – i.
- Multiplication: Use the distributive property. Each part of one complex number is multiplied by each part of the other. Remembering that i^2 = -1 is crucial for simplification. Multiplying (2 + 3i) and (1 + 4i), we end up with -10 + 11i.
- Division: To divide complex numbers, eliminate the imaginary part from the denominator by multiplying both numerator and denominator by the conjugate of the denominator. For instance, (2 + 3i) divided by (1 + 4i) is simplified by multiplying with (1 – 4i).
- Magnitude: The magnitude of a complex number a + bi is √(a^2 + b^2), showing how far it is from the origin in the complex plane.
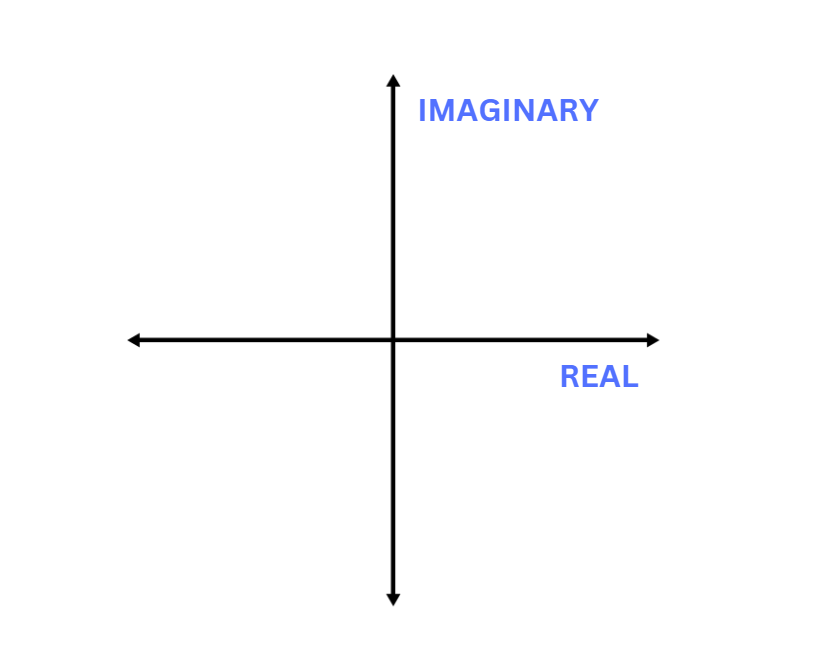
Visualizing on the Complex Plane
Complex numbers can be represented on a plane. The horizontal axis shows the real part, while the vertical axis shows the imaginary part. Every complex number finds a unique position on this plane.
Conclusions
Far from being just a mathematical curiosity, complex numbers have real-world applications. They’re used in electrical engineering, physics, and computer science, especially in situations involving oscillations and waves, like alternating current circuits.
Complex numbers, expressed as a + bi, are more than just an expansion of the number system. They enable us to solve problems that can’t be addressed with real numbers alone. From their unique arithmetic properties to their representation on the complex plane, complex numbers are a vital tool in both theoretical and applied sciences, bridging the gap between abstract mathematics and practical solutions in various fields.


